Ohm's Law is a formula used to calculate the relationship between voltage, current and resistance in an electrical circuit.
To students of electronics, Ohm's Law (E = IR) is as fundamentally important as Einstein's Relativity equation (E = mc²) is to physicists.
E = I x R
When spelled out, it means voltage = current x resistance, or volts = amps x ohms, or V = A x Ω.
Named for German physicist Georg Ohm (1789-1854), Ohm's Law addresses the key quantities at work in circuits:
| Quantity | Ohm's Law symbol | Unit of measure (abbreviation) | Role in circuits | In case you're wondering: |
|---|---|---|---|---|
| Voltage | E | Volt (V) | Pressure that triggers electron flow | E = electromotive force (old-school term) |
| Current | I | Ampere, amp (A) | Rate of electron flow | I = intensity |
| Resistance | R | Ohm (Ω) | Flow inhibitor | Ω = Greek letter omega |
If two of these values are known, technicians can reconfigure Ohm's Law to calculate the third. Just modify the pyramid as follows:
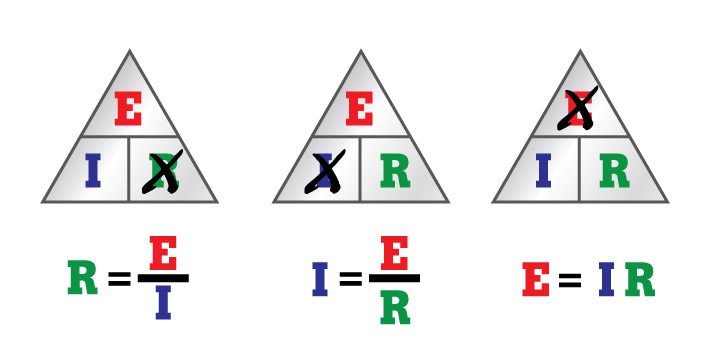
If you know voltage (E) and current (I) and want to know resistance (R), X-out the R in the pyramid and calculate the remaining equation (see the first, or far left, pyramid above).
Note: Resistance cannot be measured in an operating circuit, so Ohm's Law is especially useful when it needs to be calculated. Rather than shutting off the circuit to measure resistance, a technician can determine R using the above variation of Ohm's Law.
Now, if you know voltage (E) and resistance (R) and want to know current (I), X-out the I and calculate the remaining two symbols (see the middle pyramid above).
And if you know current (I) and resistance (R) and want to know voltage (E), multiply the bottom halves of the pyramid (see the third, or far right, pyramid above).
Try a few sample calculations based on a simple series circuit, which includes just one source of voltage (battery) and resistance (light). Two values are known in each example. Use Ohm's Law to calculate the third.
Example 1: Voltage (E) and resistance (R) are known.
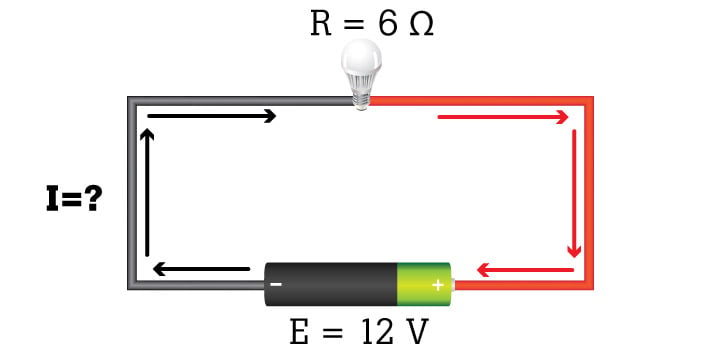
What is the current in the circuit?
I = E/R = 12V/6Ω = 2A
Example 2: Voltage (E) and current (I) are known.
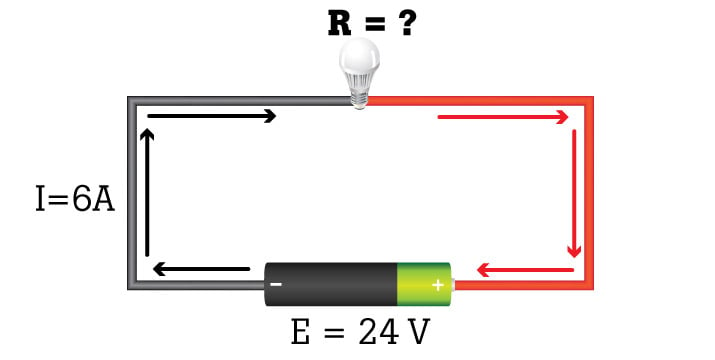
What is the resistance created by the lamp?
R = E/I = 24V/6A = 4Ω
Example 3: Current (I) and resistance (R) are known. What is the voltage?
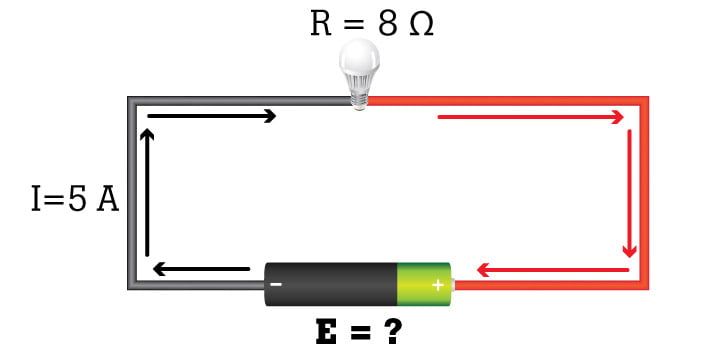
What is the voltage in the circuit?
E = I x R = (5A)(8Ω) = 40 V
When Ohm published his formula in 1827, his key finding was that the amount of electric current flowing through a conductor is directly proportional to the voltage imposed on it. In other words, one volt of pressure is required to push one amp of current through one ohm of resistance.
What to validate using Ohm’s Law
Ohm’s Law can be used to validate the static values of circuit components, current levels, voltage supplies, and voltage drops. If, for example, a test instrument detects a higher than normal current measurement, it could mean that resistance has decreased or that voltage has increased, causing a high-voltage situation. This could indicate a supply or circuit issue.
In direct current (dc) circuits, a lower than normal current measurement could mean that the voltage has decreased, or circuit resistance has increased. Possible causes for increased resistance are poor or loose connections, corrosion and/or damaged components.
Loads within a circuit draw on electrical current. Loads can be any sort of component: small electrical devices, computers, household appliances or a large motor. Most of these components (loads) have a nameplate or informational sticker attached. These nameplates provide safety certification and multiple reference numbers.
Technicians refer to nameplates on components to learn standard voltage and current values. During testing, if technicians find that customary values do not register on their digital multimeters or clamp meters, they can use Ohm's Law to detect what part of a circuit is faltering and from that determine where a problem may lie.
The basic science of circuits
Circuits, like all matter, are made of atoms. Atoms consist of subatomic particles:
- Protons (with a positive electrical charge)
- Neutrons (no charge)
- Electrons (negatively charged)
Atoms remain bound together by forces of attraction between an atom's nucleus and electrons in its outer shell. When influenced by voltage, atoms in a circuit begin to reform and their components exert a potential of attraction known as a potential difference. Mutually attracted loose electrons move toward protons, creating a flow of electrons (current). Any material in the circuit that restricts this flow is considered resistance.
Reference: Digital Multimeter Principles by Glen A. Mazur, American Technical Publishers.